Définitions des ensembles de nombre

Les entiers naturels sont les nombres entiers positifs que nous utilisons pour dénombrer des éléments discrets, comme le nombre d’élèves dans une classe ou le nombre de pommes dans un panier.
Ils commencent à ##0## et continuent sans fin, par exemple : ##0, 1, 2, 3, 4, 5, 6…##
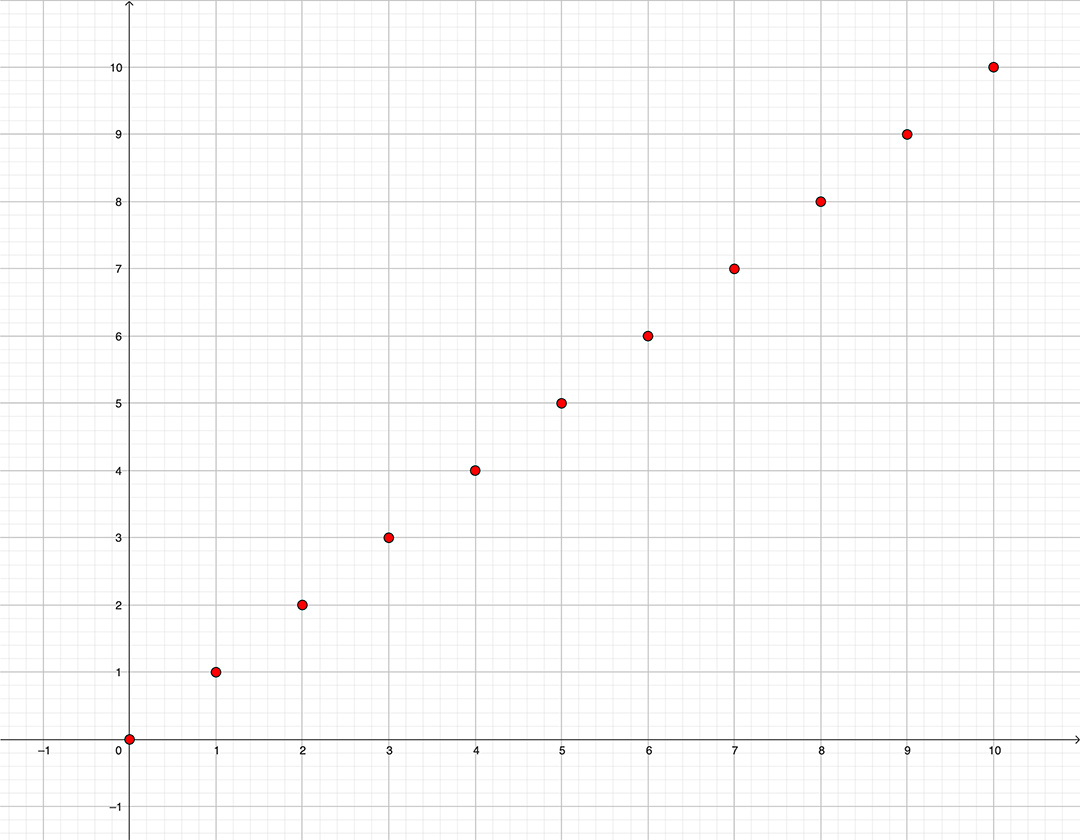
Sur le graphique ci-dessous, on retrouve les entiers naturels de 0 à 10, chaque point ayant les coordonnées ##(x,x)## où ##x \in \mathbb{N}##

Définition:
On appelle ensemble des entiers naturels l’ensemble noté ##\mathbb{N}##, défini par les deux règles suivantes :

• Axiome de base: ##0## appartient à ##\mathbb{N}##, on le notera: ##0 \in \mathbb{N}##

• Axiome de récurrence: si un nombre ##n## appartient à ##\mathbb{N}##, alors son successeur ##n + 1## appartient aussi à ##\mathbb{N}##, on le notera: si ##n \in \mathbb{N}##, alors ## n + 1 \in \mathbb{N}##

Cette définition repose sur le principe de récurrence, permettant de construire l’ensemble ##\mathbb{N}## en partant de ##0## et en ajoutant successivement ##1##.

Les nombres relatifs regroupent tous les nombres entiers positifs, négatifs, ainsi que zéro.
Ils permettent de représenter des situations où des valeurs peuvent être positives ou négatives, comme les températures, solde du compte bancaire, par exemple : ## …, – 5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, …##
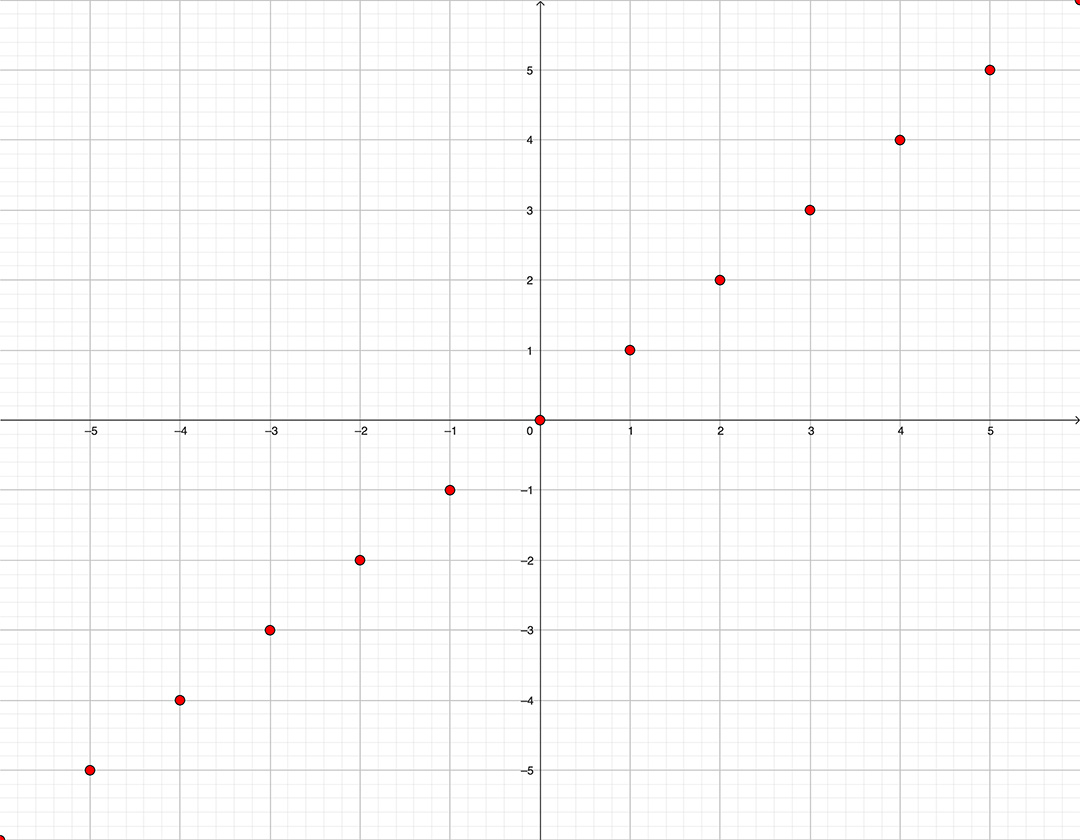
Sur le graphique ci-dessous, on retrouve les entiers relatifs de -5 à 5, chaque point ayant les coordonnées ##(x,x)## où ##x \in \mathbb{Z}##

Ce sont les nombres positifs ou négatifs sans partie décimale. Pour l’instant, un nombre négatif revêt un caractère abstrait mais tu vas vite comprendre avec un exemple :

• Étage -3 : cela signifie 3 étages en dessous de 0, c’est-à-dire au troisième sous-sol.

• Le solde d’un compte vaut -2500€, cela signifie que la personne titulaire de ce compte a un découvert de 2500€ à la banque: son solde est négatif.

Définition:
On appelle ensemble des entiers relatifs l’ensemble noté ##\mathbb{Z}##, défini de la façon suivante :

où :

• ##\mathbb{N}^*## désigne l’ensemble des entiers naturels strictement positifs (##\mathbb{N}^* = {1, 2, 3, … })##

• pour tout ##n \in \mathbb{N}^*##, l’élément ##-n## appartient aussi à ##\mathbb{Z}##

Les nombres décimaux sont des nombres (positifs ou négatifs) qui peuvent s’écrire avec un nombre fini de chiffres après la virgule.
L’ensemble des nombres décimaux se note ##\mathbb{D}## (même si ce symbole n’est pas toujours universellement utilisé).
Un nombre décimal peut être :

• Un nombre entier (comme ##-3; 5; 348##)

• Un nombre avec une partie décimale (comme ##-3,78; 2.0; 16,98789##)

Les nombres rationnels sont des nombres qui peuvent s’écrire sous la forme d’une fraction :

C’est-à-dire :

• ##a## est un entier relatif (positif, négatif ou nul)

• ##b## est un entier relatif (positif, négatif mais jamais zéro)

Un nombre rationnel est donc simplement un nombre qui peut être écrit comme le quotient de deux entiers.
L’ensemble des nombres rationnels se note ##\mathbb{Q}##

Exemples de nombres rationnels:

• ##5## car ##5 = \frac{5}{1}##

• ##-2## car ##-2 = \frac{-2}{1}##

• ##0,75## car ##0,75 = \frac{3}{4}##

• ##-3,75## car ##-3,75 = \frac{-7}{2}##

• ##\frac{2}{3}## car il est déjà sous la forme de fraction

Les nombres irrationnels sont des nombres qui ne peuvent pas s’écrire sous la forme d’une fraction ##\frac{a}{b}## où ##a \in \mathbb{Z}## et ##b \in \mathbb{Z}, b \neq 0##.
En d’autres termes :

• Ce ne sont pas des nombres rationnels 😄

• Leur écriture décimale est infinie et non périodique (elle ne forme pas de motif répétitif).

C’est-à-dire qu’un nombre irrationnel est un nombre qui a une infinité de chiffres après la virgule et dont les chiffres ne se répètent jamais.

Exemples de nombre irrationnels :

• ##\pi = 3,1415926535…## (suite infinie et non périodique)

• ##\sqrt{2} = 1,414213562…## (également une suite infinie et non périodique)

• ##\sqrt{3} = 73205080…##

• ##\sqrt{5} = 23606797…##

• ##e = 2,71828…##

On appelle nombres réels l’ensemble de tous les nombres ou encore l’ensemble de toutes les suites décimales (limitées ou illimitées) positives ou négatives.
L’ensemble des nombres réels est noté ##\mathbb{R}##

On peut dire que l’ensemble des réels ##\mathbb{R}## est constitué de :

• L’ensemble des nombres naturels ##\mathbb{N}##

• L’ensemble des nombres relatifs ##\mathbb{Z}##

• L’ensemble des nombres décimaux ##\mathbb{D}##

• L’ensemble des nombres rationnels ##\mathbb{Q}##

• L’ensemble des nombres irrationnels ##\mathbb{R \ Q}##

Mais attention, car :

• ##\mathbb{N}## est inclus dans ##\mathbb{Z}##, on le note ##\mathbb{N} \subset \mathbb{Z}##

• ##\mathbb{Z}## est inclus dans ##\mathbb{D}##, on le note ##\mathbb{Z} \subset \mathbb{D}##

• ##\mathbb{D}## est inclus dans ##\mathbb{Q}##, on le note ##\mathbb{D} \subset \mathbb{Q}##

Il n’y a donc pas besoin d’écrire toutes les inclusions, on pourra simplement écrire que les nombres réels sont l’union des rationnels et des irrationnels :

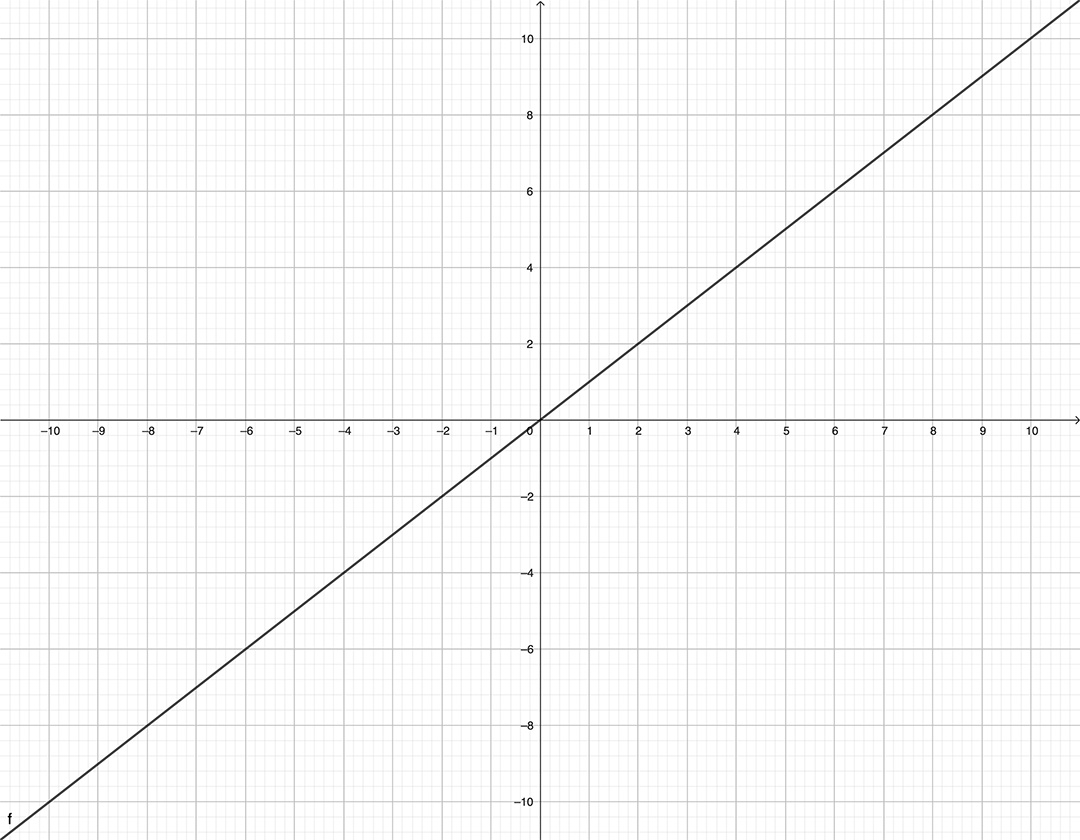
Sur le graphique ci-dessous, ils représentent une droite graduée, sans « trous » où chaque point sur la droit possède les coordonnées ##(x,x)## où ##x \in \mathbb{R}##